Build a tree in Hyperiax

All the functions of Hyperiax are about trees. Thus, it is necessary to know how to actually build a tree in Hyperiax. This notebook will show you two main ways of building trees which should meet your needs in most of the cases:

Build a tree with a defined topology
Build a tree from Newick strings

A tree in Hyperiax is instantiated from the HypTree class defined in hyperiax.tree.tree.py, which is essentially a linked list by tree nodes as TopologyNode. When initializing the HypTree, Hyperiax will automatically do all the work including assigning data according to the desired topological order, precomputing a series of indices that is required for the execution engine to run on the tree, or other functions for tree visualizations.

The topology of the tree can be simply specified by some predefined functions in hyperiax.tree.topology.py, so that you don’t need to arrange them by hands. Let’s first see how we can create and plot trees with simple topologies.

[1]:

import hyperiax
from hyperiax.tree.topology import symmetric_topology, asymmetric_topology, read_topology, write_topology
from hyperiax.tree import HypTree
from hyperiax.plotting import plot_tree

import jax
from jax import numpy as jnp

Build a tree with a simple topology

Choose the topology

The shape of the tree is determined by the topology. Take an asymmetric tree as an example, to build an asymmetric tree, with h depth and branchings, use hyperiax.tree.topology.asymmetric_topology(depth). Note that before the branch lengths have been specified explicitly, the lengths are set to be uniform by default

[2]:

topology = asymmetric_topology(5)
tree = HypTree(topology)
plot_tree(tree)

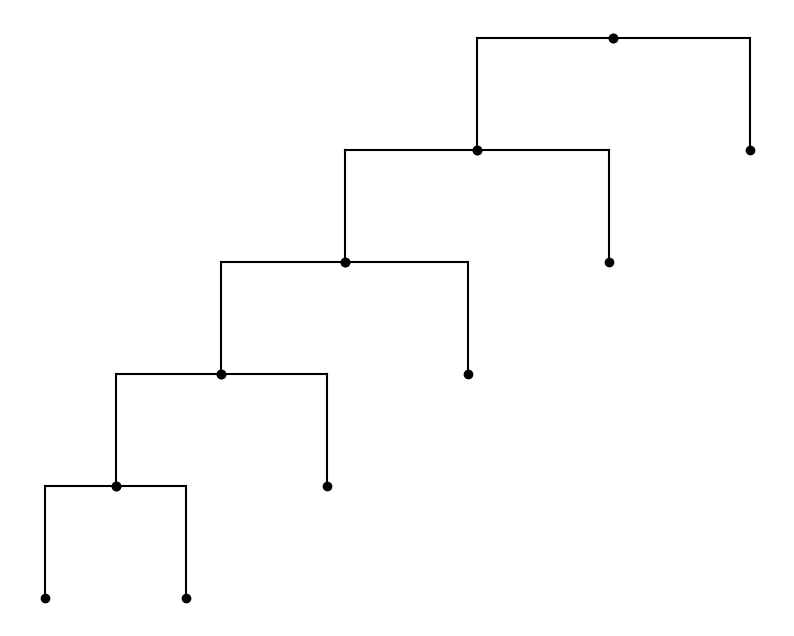
../_images/notebooks_tree_building_3_0.png

Add node names

It is also possible to add names to the tree nodes to distinguish them. The names of nodes are recorded as the attributes of TopologyNode, therefore, can be accessed and changed through iterating over all the nodes. We use a symmetric tree to illustrate it.

[3]:

# build a symmetric tree of height 4 and degree 2
topology = symmetric_topology(height=4, degree=2)
tree = HypTree(topology)

# iterate over all the nodes in the tree and assign them a name
for i,node in enumerate(tree.iter_topology_bfs()):
    node.name = 'node' + str(i)
    # alternatively the below will yield the same result but save an enumeration
    # node.name = node.id

plot_tree(tree,inc_names=True)

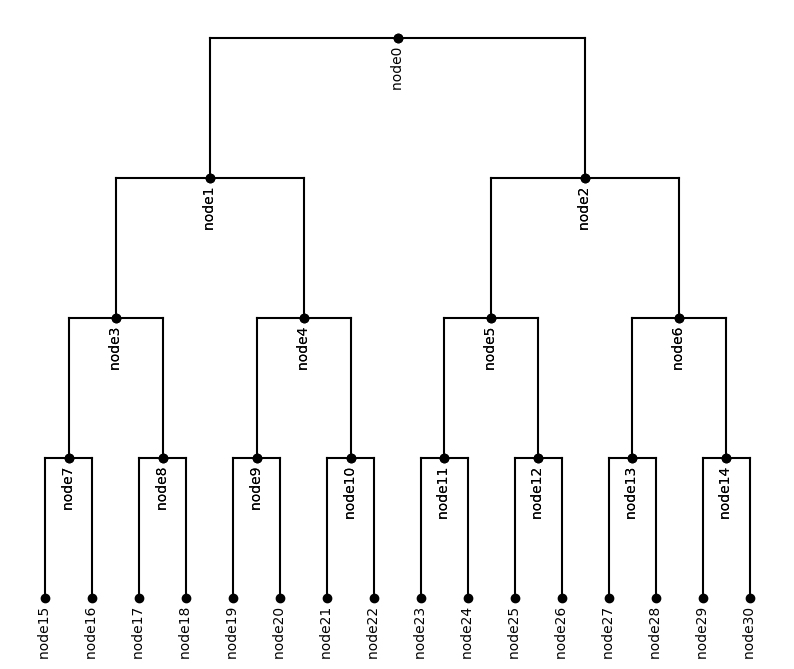
../_images/notebooks_tree_building_5_0.png

Add edge lengths

Besides the node names, all the other properties including the edge lengths are stored in TopologyNode’s data attribute, which is a dictionary. It means you can assign and access these properties using their names as keys, and the value can be either constants read from files or expressions you want to compute, just like what you can do in a normal Python dict. Here, we use decaying exponential lengths based on the depth of nodes, such that nodes closer to the leaves have shorted edge lengths.

Since each HypTree will calculate the depth of each node, we can use them here. The depth of nodes is returned as a jax.numpy.ndarray that holds a single integer, and it is stored in the same order as the rest of the data in the tree. Thus, we can use it freely to do the computations or assign it to any data slot.

[4]:

tree.add_property('edge_length', shape=(1,))
tree.data['edge_length'] = jnp.exp(-jnp.log(2)*tree.node_depths)
plot_tree(tree)

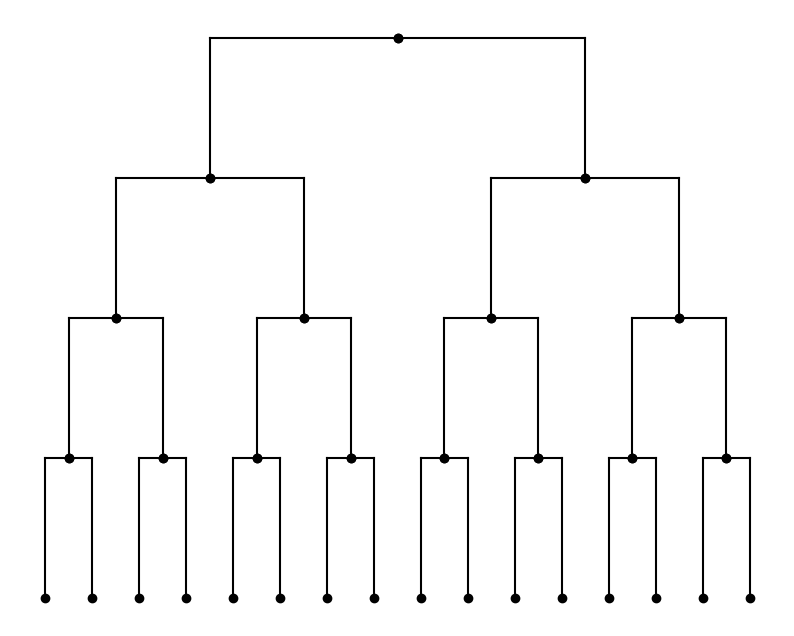
../_images/notebooks_tree_building_7_0.png

Build a tree from a Newick string

For some trees with complex topologies that can not be included into symmetric_topology or asymmetric_topology, Hyperiax also provides the function that can directly create the tree by read the Newick string which is a way of representing graph-theoretical trees with edge lengths using parentheses and commas. The Newick format is commonly used in phylogenetics, which means it can be easily downloaded from a lot of phylogenetic databases and read by Hyperiax.

A handwritten Newick tree

Let’s start from a simple Newick string: '(((A:1,B:1)H:0.5,(C:1,D:2)I:0.5)L:0.1,((E:1,F:1,G:1)J:0.5, K:0.5)M:0.1)N;'. This string is totally enough to tell us all the information about this tree:

The tree has height of 4
The tree has 8 leaves named after A, B, C, D, E, F, G, K, and except node D and K, all the leaf nodes have same edge lengths of 1, and D has 2, K has 0.5
The root of tree is called N
The inner nodes are called H, I, J, L, M, individually

Let’s create this tree with hyperiax.tree.topology.tree_from_newick_recursive(newick_string) and verify it.

[5]:

newick_string = '(((A:1,B:1)H:0.5,(C:1,D:2)I:0.5)L:0.1,((E:1,F:1,G:1)J:0.5, K:0.5)M:0.1)N;'
tree = read_topology(newick_string)
plot_tree(tree,inc_names=True)

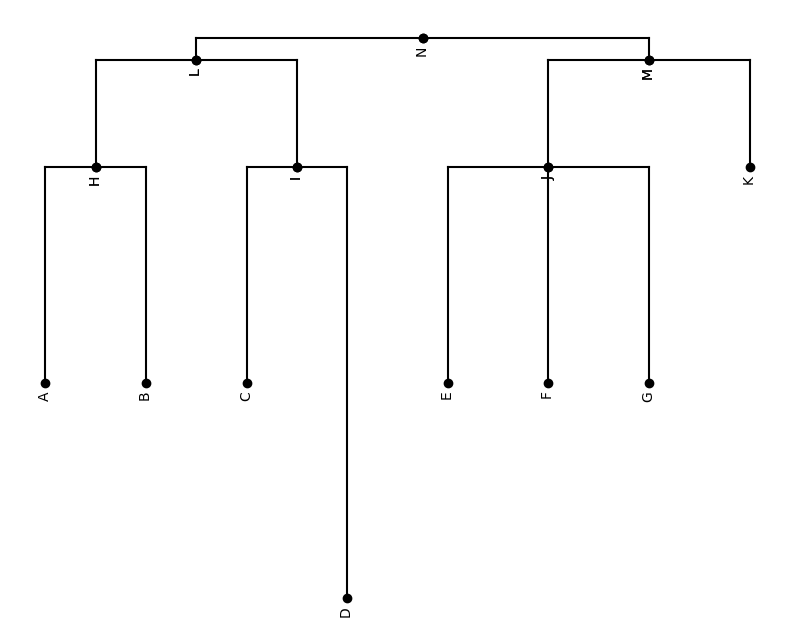
../_images/notebooks_tree_building_9_0.png

This is exactly what we are expecting!

A real phylogenetic tree

Now it’s time to work on something real. Here is the Newick string of a smaller subset of the tree from Kawahara 2023 (DOI: 10.1038/s41559-023-02041-9), let’s check if Hyperiax can make it.

[6]:

string_tree = "(Baronia_brevicornis:0.1711,((Iphiclides_podalirius:0.08472,((Graphium_evemon:0.06883,(Graphium_sarpedon:0.05466,Graphium_agamemnon:0.05188)QS1811:0.01369)QS1810:0.06096,Protographium_marcellus:0.09227)QS1808:0.01315)QS1807:0.0653,(((Hypermnestra_helios:0.04444,(Parnassius_orleans:0.01792,Parnassius_honrathi:0.03123)QS1821:0.0276)QS1820:0.06041,((Archon_apollinus:0.03581,Luehdorfia_puziloi:0.03646)QS1826:0.03388,(Sericinus_montela:0.08969,(Zerynthia_polyxena:0.02408,Allancastria_cerisyi:0.02345)QS1831:0.03039)QS1828:0.03093)QS1825:0.01972)QS1819:0.02572,(Teinopalpus_imperialis:0.09583,(((Battus_polydamas:0.0359,Battus_belus:0.04337)QS1835:0.08774,(Pharmacophagus_antenor:0.07956,(((Trogonoptera_brookiana:0.03698,(Troides_rhadamantus:0.02074,Ornithoptera_richmondia:0.01965)QS1840:0.02241)QS1839:0.00805,((Euryades_corethrus:0.04833,(Parides_agavus:0.03072,(Parides_photinus:0.02647,Parides_eurimedes:0.02819)QS1844:0.0108)QS1843:0.01245)QS1842:0.00564,Cressida_cressida:0.07354)QS1841:0.01338)QS1838:0.00944,((Byasa_alcinous:0.02248,(Atrophaneura_semperi:0.01043,Atrophaneura_dixoni:0.01171)QS1847:0.0129)QS1846:0.01879,((Pachliopta_aristolochiae:0.00348,Pachliopta_kotzebuea:0.00499)QS1849:0.0278,Losaria_coon:0.02297)QS1848:0.02356)QS1845:0.00935)QS1837:0.03434)QS1836:0.03812)QS1834:0.03412,((((Papilio_aristodemus:0.03095,(Papilio_thoas:0.00907,Papilio_cresphontes:0.00884)QS1855:0.02664)QS1854:0.03683,(Papilio_slateri:0.03379,(Papilio_glaucus:0.03012,Papilio_troilus:0.03835)QS1858:0.0096)QS1856:0.01012)QS1853:0.00628,(Papilio_gigon:0.06457,((Papilio_xuthus:0.03532,(Papilio_polyxenes:0.00579,Papilio_zelicaon:0.00541)QS1866:0.02599)QS1863:0.01789,(Papilio_deiphobus:0.02135,(Papilio_protenor:0.01221,(Papilio_polytes:0.01127,(Papilio_phestus:0.00377,Papilio_ambrax:0.00325)QS1872:0.00893)QS1871:0.00991)QS1870:0.007)QS1868:0.03981)QS1862:0.00747)QS1861:0.04588)QS1852:0.05955,Meandrusa_sciron:0.09096)QS1851:0.02719)QS1833:0.01405)QS1832:0.01719)QS1818:0.02038)QS1804:0.04527)QS1803:0;"
tree = read_topology(string_tree)
plot_tree(tree,inc_names=True)
write_topology(tree)

[6]:

'(Baronia_brevicornis:0.1711,((Iphiclides_podalirius:0.0847,((Graphium_evemon:0.0688,(Graphium_sarpedon:0.0547,Graphium_agamemnon:0.0519)QS1811:0.0137)QS1810:0.0610,Protographium_marcellus:0.0923)QS1808:0.0132)QS1807:0.0653,(((Hypermnestra_helios:0.0444,(Parnassius_orleans:0.0179,Parnassius_honrathi:0.0312)QS1821:0.0276)QS1820:0.0604,((Archon_apollinus:0.0358,Luehdorfia_puziloi:0.0365)QS1826:0.0339,(Sericinus_montela:0.0897,(Zerynthia_polyxena:0.0241,Allancastria_cerisyi:0.0235)QS1831:0.0304)QS1828:0.0309)QS1825:0.0197)QS1819:0.0257,(Teinopalpus_imperialis:0.0958,(((Battus_polydamas:0.0359,Battus_belus:0.0434)QS1835:0.0877,(Pharmacophagus_antenor:0.0796,(((Trogonoptera_brookiana:0.0370,(Troides_rhadamantus:0.0207,Ornithoptera_richmondia:0.0196)QS1840:0.0224)QS1839:0.0081,((Euryades_corethrus:0.0483,(Parides_agavus:0.0307,(Parides_photinus:0.0265,Parides_eurimedes:0.0282)QS1844:0.0108)QS1843:0.0125)QS1842:0.0056,Cressida_cressida:0.0735)QS1841:0.0134)QS1838:0.0094,((Byasa_alcinous:0.0225,(Atrophaneura_semperi:0.0104,Atrophaneura_dixoni:0.0117)QS1847:0.0129)QS1846:0.0188,((Pachliopta_aristolochiae:0.0035,Pachliopta_kotzebuea:0.0050)QS1849:0.0278,Losaria_coon:0.0230)QS1848:0.0236)QS1845:0.0093)QS1837:0.0343)QS1836:0.0381)QS1834:0.0341,((((Papilio_aristodemus:0.0310,(Papilio_thoas:0.0091,Papilio_cresphontes:0.0088)QS1855:0.0266)QS1854:0.0368,(Papilio_slateri:0.0338,(Papilio_glaucus:0.0301,Papilio_troilus:0.0384)QS1858:0.0096)QS1856:0.0101)QS1853:0.0063,(Papilio_gigon:0.0646,((Papilio_xuthus:0.0353,(Papilio_polyxenes:0.0058,Papilio_zelicaon:0.0054)QS1866:0.0260)QS1863:0.0179,(Papilio_deiphobus:0.0214,(Papilio_protenor:0.0122,(Papilio_polytes:0.0113,(Papilio_phestus:0.0038,Papilio_ambrax:0.0033)QS1872:0.0089)QS1871:0.0099)QS1870:0.0070)QS1868:0.0398)QS1862:0.0075)QS1861:0.0459)QS1852:0.0595,Meandrusa_sciron:0.0910)QS1851:0.0272)QS1833:0.0141)QS1832:0.0172)QS1818:0.0204)QS1804:0.0453)QS1803:0.0000;'

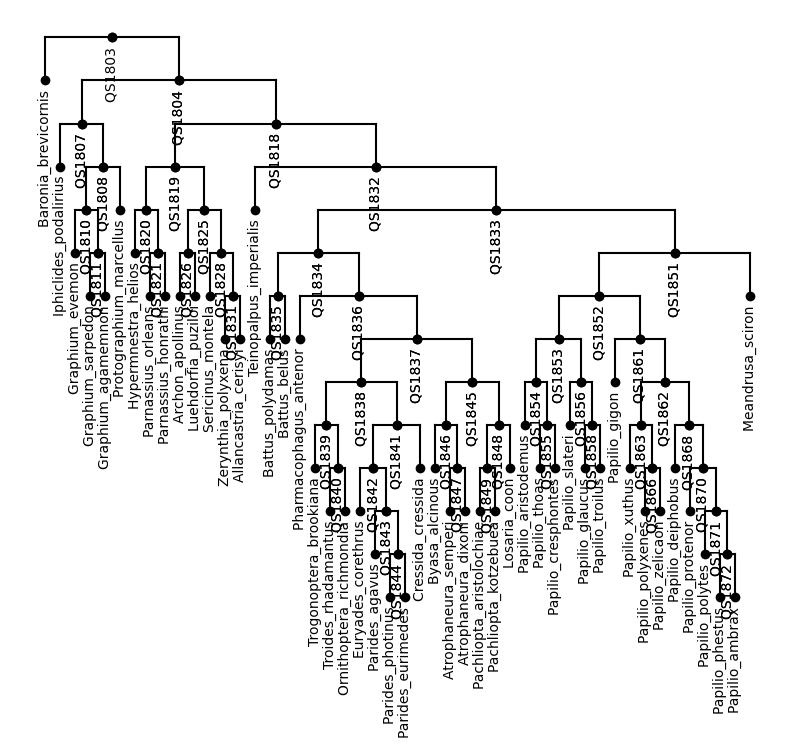
../_images/notebooks_tree_building_11_1.png

It works!

Summary

In this notebook, we know how to create a tree in Hyperiax, from either predefined topology or Newick strings. In the next one, we will see how to define some basic executions on the tree, and appreciate how fast and easy you can do this with Hyperiax.